Step-by-step derivation of the physically-based computer-generated hologram formula

This guide assumes the reader already knows what a hologram is and, in broad terms, the basic principles of how to make one.

Let's say we have a 3D object, and we want to make a computer-generated hologram from it. To do that, we first decompose the object into a large number of points, which we approximate as spherical light sources. (For now, we'll ignore the opacity of the object. This means that the points near the holographic plate don't block the light from the farther ones).

The light from all these points will compose what we'll call the object wave, which has a very complex shape. But to make the hologram, we also need a (much simpler) reference wave, which will act as the "key" to later decode the interference pattern that will result from the mix of both waves hitting the holographic plate, and thus reconstruct the 3D image from the hologram.

The reference wave we'll use is a plane wave, which means it can be thought of as a series of parallel planes, spread apart by the wavelength $\lambda$, each corresponding to a crest in the reference wave.

Our system of coordinates to describe the 3D space will be the left-handed Cartesian, with X pointing to the right, Y pointing up, and Z pointing forward (from the object to the hologram). The holographic plate will be a rectangular area centered at the origin of the system of coordinates, and perpendicular to the Z axis (i.e., it will be contained the XY plane).

Given the above, we'll define the following basic elements for our calculations:

• $h = (h_x, h_y, 0)$, a point on the hologram plane ($z = 0$), and
• $p_n = (p_{nx}, p_{ny}, p_{nz})$, the location of the $n^{th}$ object point light source.

Step 1: Building the object wave

To start, let's recall, as previously described, that the oscillation of a light wave generated by a point light source, at instant $t$, can be described with:

...where $A$ is the amplitude (maximum height) of the oscillation, $\omega$ is the temporal angular frequency of the wave (i.e. how many cycles, in radians, the wave completes per unit of time) and $\varphi$ is the initial phase (angle at $t=0$) of the wave at the point where we're measuring it.

Using this formulation, the amplitude of the whole compound object wave, made up of all the object points' individual waves, at a given point $h$ of the hologram and a given time $t$, is given by simply summing all contributions together:

The value of $\varphi_n$ at point $h$ depends on the distance from the object point to the hologram point being considered, which is calculated using the familiar Euclidean distance formula:

(remember that $h_z$ is zero, because we placed the hologram plane at $z=0$).

This distance (which nothing more than the radius of the light sphere emitted from the $n^{th}$ point) is then multiplied by the spatial angular frequency of the wave (i.e. how many cycles, in radians, the wave completes per unit of distance), which is abbreviated as $k = \tau/\lambda$, and —somewhat unhelpfully— called the "wavenumber".

In this guide, we'll use $\tau$ as a symbol for $2\pi$, for the reasons described in the Tau Manifesto.

This multiplication, $k d_n(h)$, like the $\omega t$ one, yields a phase angle, so both values can be subtracted to yield the phase of the wave $p_n$ at point $h$ and instant $t$.

The object wave formula then becomes:

Note how the duality of this generic formula can be exploited, on the one hand, to calculate both the variation of the object wavefront in space (i.e. across the hologram), at a given instant frozen in time, by varying $h$ and keeping $t$ constant, and, on the other hand, to calculate the variation of the object wavefront at a fixed hologram point, by varying $t$ and keeping $h$ constant.

Step 2: Adding the reference wave

As may be noted, the above formula is just for the compound object wave. We still need to add the reference wave to get the final wavefront that will form the hologram.

As mentioned above, we'll be using a planar wave as the reference wave (which makes some calculations simpler and some practical setups easier), so it's not useful to describe it with the spherical wave formula, because by definition, a planar wave is the idealized limit of a spherical wave as its source point's distance from the measuring region grows toward infinity, with the local curvature of its wavefronts consequently approaching zero. What we do, instead, is define it by the angles it makes with the hologram plane, since these will be constant.

This is done using two angles: $\theta_y$, aka "yaw", which represents the planar wave's rotation around the (vertical) Y axis (like a head turning side to side), and $\theta_x$, aka "pitch", which represents its rotation around the (horizontal) X axis (like a head nodding up and down).

Let's start by setting $\theta_x$ to zero and seeing what happens as we change $\theta_y$. The following image displays a top view of the setup: we can see the planar wave, with its successive crests shown as parallel lines, and the holographic plate in dark gray.

As we can figure out from the image, if we adjust the angle $\theta_y$, although the wavelength $\lambda$ would remain the same, the distance between two wave crests in the hologram plane would change accordingly. In other words, this distance is the projection of $\lambda$ into the X axis. We'll call this $\lambda_x$.

Using elementary trigonometry, we can see that, from the definition of the sine of an angle as opposite/hypotenuse, we obtain the relationship $\sin(\theta_y) = \lambda/\lambda_x$, and therefore, $\lambda_x = \lambda/\sin(\theta_y)$.

Now, knowing the projected wavelength of the reference wave along the hologram plane, we can, for every location $h_x$, obtain the phase of the wave. For example, assuming the wave's phase at $h_x=0$ is zero, the wave completes a full cycle (i.e. its phase returns to zero) at $h_x=\lambda_x$, and again at $2 \lambda_x$, $3 \lambda_x$, etc. So, to get the reference wave phase at any given $h_x$, we just divide it by $\lambda_x$, as that's our "unit".

Of course, this gives us a fractional value, a linearly growing value representing the number of cycles completed as we advance $h_x$. To pass this value to the cosine function and thus get the amplitude of the wave, we need to convert this to radians, which we do by multiplying the fractional value by $\tau$. The formula for a (yaw-varying only) reference wave is thus:

The same reasoning can be made for the case where we vary $\theta_x$ and keep $\theta_y=0$ — we obtain $\lambda_y = \lambda / \sin(\theta_x)$. So putting it all together, for the general case where both $\theta_x \neq 0$ and $\theta_y \neq 0$:

By rearranging the pieces, and because $k=\tau/\lambda$, this simplifies to:

To make this similar to the object wave function, we can abstract away the inner sum that's multiplied by $k$ into a function $d_ʀ$ (named that way because, like the function with the same name for the object wave, it provides the distance that determines the location of the wave's crests in the hologram):

thus yielding the reference wave formula:

Step 3: Putting the pieces together

Ok, now that we have the object and the reference wave described as simple formulas, we can compute the hologram. To do that, we simply go over each point $h$ in the hologram, and sum the object and the reference waves, obtaining the interference field $E$:

which, when combined with equations \eqref{eq:obj} and \eqref{eq:ref}, expands to:

However, this only gives us the instantaneous interference pattern created from the interaction of all these waves at a given moment $t$. The actual hologram is the result of the static "nodes" that appear over time when coherent waves interact. These nodes will always have zero activity, while other points in the hologram will register oscillations.

The image below illustrates this effect:

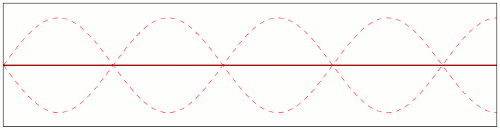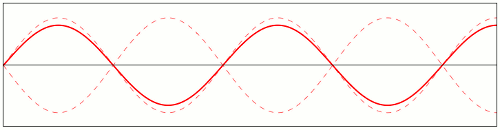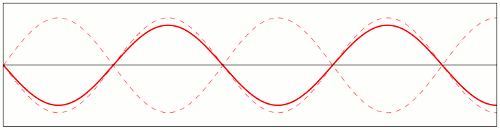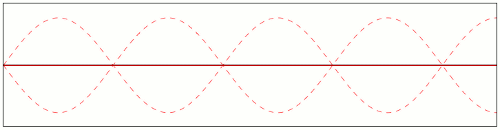
Such nodes form whenever several waves of the same (constant) frequency interact. In fact, this is exactly the principle that allows holograms to exist, as static snapshots of a dynamic interference pattern. To gain a better understanding of how these nodes form, play a little with the animation at this page.

Now, although these oscillations have all the same period (because the waves are coherent), their peaks and valleys will occur at different stages of the "global" cycle. And each of these oscillation zones will have the value zero at the right time in their cycle. So that makes it impossible, in an instant snapshot, to distinguish permanently static zones from zones that only happen to be passing through zero at that moment.

To solve this, we have to calculate the interference pattern for all possible phase positions of the global cycle and accumulate any activity, to make the oscillation zones unambiguously distinguishable from the static nodes of the interference pattern.

The straightforward way to do that is to discretize the phase space into a finite set of regularly-spaced phase values, calculate the instantaneous interference pattern at each phase value, and sum them all to yield the cumulative interference pattern, a.k.a. the hologram.

Now, "discretize the phase space" may sound fancy, but in practice, this is equivalent to calculating the instantaneous intensity for all instants contained in the duration of a wave cycle (subdividing this period of time into a convenient number of time steps), since each instant will correspont to a phase position, and these will repeat after the wave cycle is over (so a single cycle is enough to cover all the phase positions).

One thing to keep in mind when summing these values is that, because each oscillation in the pattern occurs over the same length of time, and because the oscillations consist in the wave alternating between positive and negative values, simply summing the interference pattern over a wave cycle would result in zero everywhere. We need to make sure the values we're summing actually accumulate, rather than cancel out.

Fortunately, what the holographic plate registers is intensity, not amplitude, and intensity is proportional to the amplitude squared; the squaring, conveniently, provides us with only positive values, which can indeed be summed and accumulated properly.

The cumulative interference pattern (i.e., the actual hologram) is thus obtained by:

This is all we need to make the hologram! Since we're talking about computer-generated holograms, it is appropriate to present the above equation in the form of a computer algorithm. So, in pseudo-code, the final equation above translates to something like this:

	var timeSteps = 100
	var holoPixels = 500
	var objectPoints = [
	      {x: ..., y: ..., z: ...},
	      {x: ..., y: ..., z: ...},
	      {x: ..., y: ..., z: ...} ]
	var amplitude[], intensity[], hologram[]

	for t = 0 --> timeSteps {
	  ph = t/timeSteps * 2*pi  # wave phase, from 0 to 2pi
	  for px = 0 --> holoPixels {
	    amplitude[ px ] += ref-amplitude( px, ph )
	    for each pt in objectPoints {
	      amplitude[ px ] += obj-amplitude( px, ph, pt )
	    }
	    intensity[ px ] = amplitude[ px ]^2
	  }
	  hologram[] += intensity[]
	}

	# Normalize
	hologram[] /= max( hologram[] )

	# Auxiliary functions
	ref-amplitude( px, ph ) {
	  ...
	}
	obj-amplitude( px, ph, pt ) {
	  ...
	}
	

But this is a rather naive approach, which not only introduces a loss of precision in the quantization of both space (by dividing the object in points and the hologram surface in pixels) and time (by dividing the phase space into discrete steps), but also requires the calculation to range over a given length of time — in other words, it essentially simulates an exposure period.

In the next chapter, we will explore ways to make this calculation both more exact and faster. Onward!